does not exist.
Each problem is worth 10 points. Show all work for full credit. Please circle all answers and keep your work as legible as possible. No actual reindeer were harmed in the making of this exam.
If we approach along the line x = 0 (the y axis),
this becomes 
If instead we approach along the line y = x, we
have 
.
Since these limits don't agree as we approach the point (0,0) along different paths, the limit does not exist at that point.
Note: This was problem 11 in section 12.2.
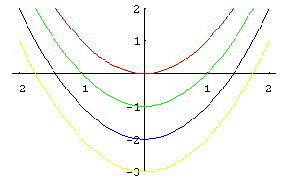
2. Sketch at least four level curves of z = x2 - y, indicating the z value of each.
If we let z = 0, the corresponding level curve is y = x2. For z = 1 we have y = x2 - 1, for z = 2 we have y = x2 - 2, and for z = 3 we have y = x2 - 3, etc. The graph below shows these curves in red, green, blue, and yellow respectively:
3. Find the directional derivative of z = x2 - y in the direction of the vector <-3,4> from the point (-2,1,3).
First we find a unit vector in the direction given. Since <-3,4> is of magnitude 5, this unit vector will be u = <-3/5,4/5>.
We also compute the gradient, and since zx = 2x and zy = -1, grad z = <2x, -1>, and at the point (2, -1) we have grad z(2, -1) = <2(-2), -1>.
Then the directional derivative 
.
4. Find an equation for the plane tangent to the sphere x2 + y2 + z2 = 72 at the point (-3, 6, -2).
First find the partial derivative (implicitly) with respect to x:
,
so 
.
Similarly, we can find that 
.
Plugging in the values for our specific point gives 
and 
.
Inserting these values into our usual equation for the tangent plane at a point gives:
z + 2 = -1.5(x + 3) + 3(y - 6).
5. The organization Reindeer Lovers International is making an effort to increase the population of reindeer in the world. Their analysis indicates that changes in the reindeer population (represented by P, in thousands) are mostly caused by changes in the food supply (represented by F, in thousands of tons) and changes in the amount of toxic chemicals (represented by C, in International Toxic Chemical Units, or just I.T.C.U.s) in the reindeer habitats. Both F and C can change over time. Preliminary studies also indicate that the rate at which increases in food supply affect population is about 1.6 reindeer per ton of food, and the rate at which toxic chemicals affect population is a loss of about 300 reindeer per I.T.C.U.
Give the appropriate version of the chain rule for 
.
If Reindeer Lovers International can provide 400 extra tons of food each
year and keep the increase of toxins down to 2 I.T.C.U.s each year, what
should be the annual change in world reindeer population?
From the description given, the "tree" (get it? No intention of offending anyone's religious sensibilities, but I thought it was kind of funny anyway) must look like:
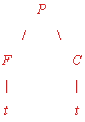
So the corresponding version of the chain rule is:
Inserting the values given in the problem in the appropriate places gives:
(1.6)(400) + (-300)(2) = 640 - 600 = 40 reindeer per year.
Note: If you take the "represented by P, in thousands"
seriously, it convolutes things a bit but the answer is still the same.
Essentially it just divides a couple of the things above by 1000, but then
multiplies something else by 1000 in a way that cancels out. I didn't mean
for this to be part of the problem, and most people blithely swept right
past it. My apologies to anyone who was troubled excessively by it!
6. Find the maximum rate of change of 
at the point (2, 1). In which direction does it occur?
The maximum rate of change will occur in the direction
of the gradient, which is
.
The easy way to get the maximum rate of
change is to know that it's given by the magnitude of the gradient. Otherwise
you can just compute the directional derivative in the direction of the
gradient, which is a messier way around. Either way it comes out to 
.
Note: This problem was taken directly from the
chapter review, as hinted in class.
7. Zeb the mosquito is hovering near the rump of an elephant (mosquitos are very self-centered, so Zeb thinks of himself as being at the origin), which from his point of view looks like the surface 5x + 2y - z = 6. Zeb intends to bite the elephant at the point nearest him. Find the coordinates of that point and the distance Zeb needs to travel to get there.
This amounts to minimizing 
,
or (much easier) minimizing 
.
Taking partials and setting them equal to zero gives the two equations 52x + 20y = 60 and 20x + 10y = 24, or some equivalents.
Solving these (there are easy ways and there are hard ways, of course) gives x = 1 and y = 2/5.
Plugging these into the original equation gives
z = -1/5, so the point Zeb wants to bite is 
.
Finally, find the distance from (0,0,0) to (1,
2/5, -1/5), which is 
.
8. Biff is a student taking calculus at OSU and he's a bit confused. Biff says "I don't believe this directional derivative stuff. I looked at the graph of this function, and you can tell that at (0,0) the slope along both the x and the y axes is zero, so both fx and fy are zero. But if you go in a direction like <1,1>, it drops off. The thing is, that formula for directional derivatives just puts together the two partial derivatives, and they're both zero at (0,0), so it'll say the directional derivative is zero too. But from the graph you can see that it doesn't stay flat when you go that way, so the directional derivative shouldn't be zero there."
Help Biff out. Either explain why he's right, or clear up his confusion by explaining to him what's wrong with his reasoning.
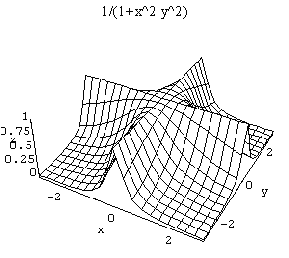
There are lots of really good ways to get at Biff's problem, of course, but mostly it boils down to him blurring the derivative (directional or otherwise) at a point with the derivative elsewhere.
Probably the best answer given, in terms of being short and to the point, was:
"The derivative is the slope of the function at
one point, so the slope at (0,0) is zero. The rest of the graph doesn't
have anything to do with the slope at (0,0)."
9. Find all critical points of functions in the family f(x,y) = xe-ax + ye-by and classify them as maxima, minima, or saddle points. Graphs of several members of this family are shown below, but note that the scales are not all the same.
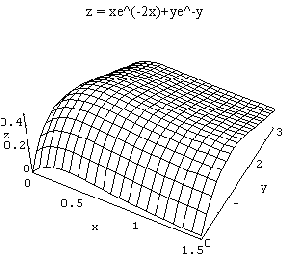
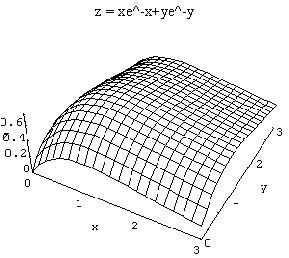
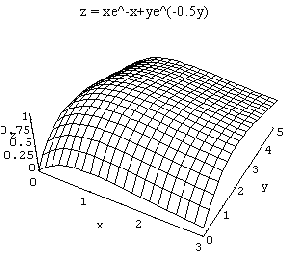
First, find the partials: fx = 1e-ax
+ xe-ax(-a) = e-ax(1-ax) and similarly fy =
1e-ay + ye-ay(-a) = e-ay(1-ay).
Setting partials equal to zero gives e-ax(1-ax) = 0, and since exponential functions are never zero it follows that 1-ax = 0, so x = 1/a. Similarly it works out that y = 1/b. This means our only critical point is (1/a,1/b).
To classify this critical point, we need the second order partials:
fxx = -ae-ax - ae-ax + -axe-ax (-a) = -2ae-ax + a2xe-ax
fxy = 0
fyy = -be-by(1-by) + e-by(-b) = -2be-by + b2ye-by
If you look close, you can see I did those two different ways -- fxx based on my first version of fx, but fyy based on my simplified fy. It wasn't 'cause I'm stupid, it was because I knew they should match and this was an easy double-check for little mistakes.
Now I bravely compute D(1/a,1/b), and I end up
with abe-2 (getting this is probably the messiest bit on the
whole exam). The sign of this depends on both a and b. When both
are positive, D is positive, and fxx is negative so we have
a local maximum, which is what we see in all the example graphs given.
When their signs are opposite, D is negative and we have a saddle point.
When their signs are both negative, D is positive but now fxx
is positive too so we have a minimum.
10. Show that the z intercept of a plane tangent to
a sphere of radius r at the point (x0, y0, z0)
is given by 
.
Sometimes it's the questions that can be stated most briefly that are the hardest.
Start with the equation for a sphere of radius r (yes, center it at the origin!), x2 + y2 + z2 = r2.
Implicitly differentiate with respect to x and
then y, as in problem 4, to get
and 
.
Plug these and the coordinates of our point into
the standard tangent plane equation to get 
.
There are two big hurdles left, and you can take
them in either order (how's that for a screwed up metaphor?). I'll take
the less tricky first: To find our plane's z intercept, I set x and y equal
to 0 and see what z value that gives me. The equation then looks like 
.
The other hurdle takes a little bit more inspiration, but the trick was
frequently used in the problems from 12.6 that this resembles. If I rearrange
that equation by multiplying both sides by z0, then shuffling
stuff to the right, I can get z z0 = x02
+ y02 + z02. This stuff on
the right-hand side of the equation is familiar -- according to the equation
for a sphere, at any point on the sphere that should equal r2.
Making this substitution gives z z0 = r2, or 
for the z intercept. Wow.
Extra Credit (5 points possible):
We know that for continuous functions fxy = fyx. Are there functions for which fxx = fyy, but without fxx or fyy being zero? Either give an example of one or explain why it couldn't happen.
There are lots of examples available, the easiest being f = x2 + y2.
There are also weirder possibilities, and I was impressed at the range people came up with, including sin(x+y), exy, sin x sin y, and any second-degree polynomial in x and y with leading coefficients equal. Yes, there's some pattern to it.
Also bear in mind that "wrong" answers aren't
worthless. Lots of people got 2 or 3 points for clear, reasoned explanations
of why it didn't seem possible.