Calculus IV Problem Set 1 Fall 1999 Due 10/1/99
1. [Based on p. 812 #57, Stewart] Two surfaces are called orthogonal
at a point of intersection if their normal lines are perpendicular at that
point.
(a) Show that surfaces with equations F(x,y,z) = 0 and G(x,y,z) = 0
are orthogonal at a point P where grad F is not equal to 0 and grad
G is not equal to 0 if and only if FxGx+FyGy+FzGz
= 0 at P.
(b) Use part (a) to show that the surfaces a2z2
= x2 + y2 and x2 + y2 + z2
= r2 are orthogonal at every point of intersection. Describe
briefly what this means about the two surfaces represented by these equations.
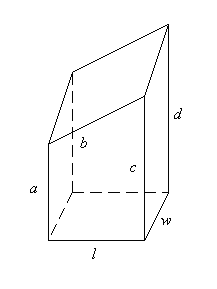 2.
Consider the solid created by diagonally slicing a rectangular box with
a plane somewhere between its base and top. Let the base have length
l
and width w, and the vertical edges be cut off with heights
a,
b,
c,
and d (and feel free to suppose that these heights are arranged
in ascending order if you like).
2.
Consider the solid created by diagonally slicing a rectangular box with
a plane somewhere between its base and top. Let the base have length
l
and width w, and the vertical edges be cut off with heights
a,
b,
c,
and d (and feel free to suppose that these heights are arranged
in ascending order if you like).
(a) Select a convenient coordinate system and find an equation for the
plane that slices the box.
(b) Did your equation for the plane in part (a) use all four values
a,
b,
c,
and d? If it did, explain what requirements there are for the values
of these heights. If it did not, find the value of the fourth in terms
of the other three.
(c) Set up an iterated integral and use it to find the volume of the
truncated box.
 2.
Consider the solid created by diagonally slicing a rectangular box with
a plane somewhere between its base and top. Let the base have length
l
and width w, and the vertical edges be cut off with heights
a,
b,
c,
and d (and feel free to suppose that these heights are arranged
in ascending order if you like).
2.
Consider the solid created by diagonally slicing a rectangular box with
a plane somewhere between its base and top. Let the base have length
l
and width w, and the vertical edges be cut off with heights
a,
b,
c,
and d (and feel free to suppose that these heights are arranged
in ascending order if you like).