1. Give parametric equations x(t), y(t), and bounds for t that produce a path from (3,0) to (5,7).
 

x(t) = 3 + 2t

y(t) = 0 + 7t

for 0 t 1
 
 
 

2. Give parametric equations x(t), y(t), and bounds for t that produce a unit circle (centered at the origin) beginning at (1,0).
 

x(t) = cos(t)

y(t) = sin(t)

0 t 2
 
 
 

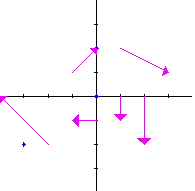
3. Plot the vector field F(x,y) = i + j for the points (0,0), (2,0), (0,2), and (-3,-2).
 

The vectors all point up and to the right.

1. Give parametric equations x(t), y(t), z(t), and bounds for t that produce a path from (-2,7, 1) to (a,b,c).
 

x(t) = -2 + (2 + a)t

y(t) = 7 + (b - 7)t

z(t) = 1 + (c - 1)t

for 0 t1
 
 
 

2. Give parametric equations x(t), y(t), and bounds for t that produce an arc of a circle (centered at the origin) of radius a beginning at (0,a) and continuing counterclockwise through n quadrants.
 

x(t) = a cos t

y(t) = a sin t

for /2 tn /2 + /2
 
 
 

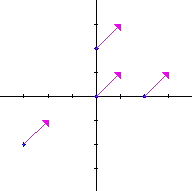
3. Plot the vector field F(x,y) = yi - xj for one point on each of the positive and negative x and y axes, and for one point in each of the four quadrants.
 

It spirals clockwise. Several representative vectors are shown below.