where F(x,y,z) = yi - xj - 2k and S is the
surface of the paraboloid z = x2 + y2 (with upward
orientation) within the cylinder x2 + y2 = 1.
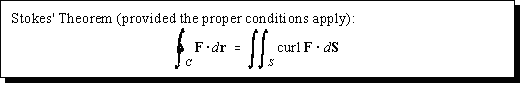
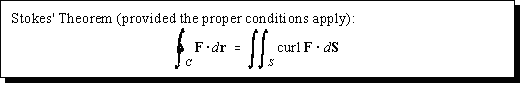
I. We parametrize the surface in our usual way, getting
x(u,v) = u
y(u,v) = v
z(u,v) = u2+v2
so r(u,v) = <u,v,u2+v2>,
for values of u and v for which u2+v2
1 (to stay within that cylinder).
II. We find F(r(u,v)) = <v, -u, -2>.
III. We find ru=<1,0,2u> and rv=<0,1,2v>, and then cross them to get ru # rv = <-2u,-2v,1>.
IV. We put the last two pieces together to form
the integral 
.
V. We dot the vectors in the integrand and convert
to polar coordinates to get 
which works out to -2pi.
2. Use Stokes' Theorem to compute 
where S is the top half of a sphere of radius 3 centered at the origin
with upward orientation and F(x,y,z) = zi + yj - xk.
By Stokes' Theorem, this surface integral is the
same as 
,
where C is the circle which forms the boundary of the hemisphere, i.e.
the circle of radius 3 centered at the origin in the xy plane. So we compute
this line integral:
I. We parametrize this circle (noting that each of its points has a z coordinate of 0 since it lies in the xy plane) as
x(t) = 3cos t
y(t) = 3sin t
z(t) = 0
so r(t) = <3cos t, 3sin t, 0> for 0
t
2pi
II. We find F(r(t)) = <0, 3sin t, -3cos t>
III. We compute r'(t) = <-3sin t, 3cos t, 0>
IV. We set up the integral 
.
V. We compute the dot product to make the integrand
9sin t cos t, and with a u=sin t substitution (or appropriate trig identity)
work this out as 0.
2'. Use Stokes' Theorem to compute 
where S is the top half of a sphere of radius 3 centered at the origin
with upward orientation and F(x,y,z) = xyi + xyj +
zk.
By Stokes' Theorem, this surface integral is the
same as 
,
where C is the circle which forms the boundary of the hemisphere, i.e.
the circle of radius 3 centered at the origin in the xy plane. So we compute
this line integral:
I. We parametrize this circle (noting that each of its points has a z coordinate of 0 since it lies in the xy plane) as
x(t) = 3cos t
y(t) = 3sin t
z(t) = 0
so r(t) = <3cos t, 3sin t, 0> for 0
t
2pi
II. We find F(r(t)) = <9cos t sin t, 9cos t sin t, 0>
III. We compute r'(t) = <-3sin t, 3cos t, 0>
IV. We set up the integral 
.
V. We compute the dot product to make the integrand -27cos t sin2 t + 27cos2 t sin t, and with a u=sin t substitution for the first term and u=cos t substitution for the second term work this out as 0.