Each problem is worth 10 points. Show all work for full credit. Please circle all answers and keep your work as legible as possible. No animals were harmed in the making of this exam.
 

1. Show that  does not exist.
 
 

2. For reasons beyond human comprehension, the radius of a big right circular cone is increasing at a rate of 1.8 in/s while its height is decreasing at a rate of 2.5 in/s. At what rate is the volume of the cone changing when the radius is 120 in. and the height is 140 in.? [Hint: ]
 
 

3. Compute the directional derivative of the function f(x,y) = xy² - x³ in the direction of the vector <-3,4> from the point (-1,-2).

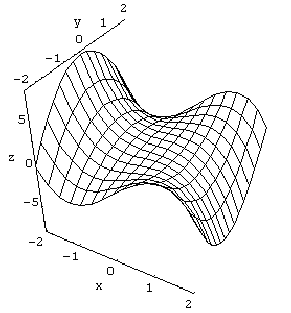
4. Find the maximum rate of change of the function f(x,y) = xy² - x³ at the point (1, 2) and the direction in which that maximum change occurs.
 
 

5. Find the critical points of the function f(x,y) = x³ - 6x - y² and classify them as maxima, minima, or saddle points. The graph might be helpful, but you can't rely on it alone -- you must show something is a saddle point, for instance, rather than just saying that it looks like one.

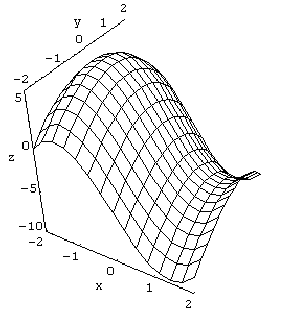
6. A group of puffins (puffins are sea birds, and while they're only distantly related to penguins some authorities have suggested that when unobserved they enjoy sliding on snow as much as penguins, and besides they have a funny name) has gone snowboarding. If a puffin is at the point (3,-5,2) on a surface shaped like the lower sheet of the hyperboloid x² + y² - (z - 8)² = -2, and the puffin's snowboard is of course tangent to the surface at that point, find an equation for the plane containing the snowboard.

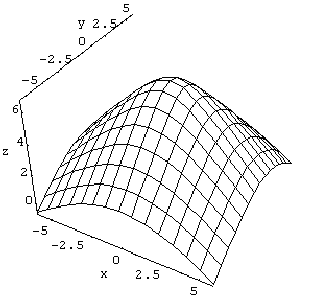
7. Buffy is a student taking calculus at Oklahoma State University, and she's a little confused. She says "Oh my God. I'm, like, just so confused about these level curve thingys, you know? I mean, it's like, if I just know that all the level curves are circles or something, I don't think I can even, like, say what the graph thingy looks like, 'cause there could be, like, totally different graphs that have the same level curves. Like, this problem we had had a picture like this, but I think there are lots of different graphs that could be like that, you know?"

Is Buffy right? Either explain to her what different surfaces might have these level curves, or explain why it couldn't happen.

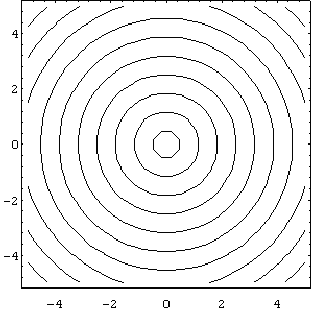
8. Show that the z-intercept of the plane tangent to the paraboloid z = x² + y² at the point (x₀, y₀) is z = -x₀² - y₀².
 
 

9. Find an expression for a vector normal to a surface f(x,y) at the point (x₀,y₀). [You may assume that the surface is continuous at this point and that the partial derivatives both exist there. The point-normal equation for a plane a(x-x₀) + b(y-y₀) + c(z-z₀) = 0 may be helpful.]
 
 

10. Find the maximum value of the plane f(x,y) = x + y subject to the constraint x² + y² = 1.
 
 

Extra Credit (5 points possible):

Problem 10 finds the highest point on the trace of a particular plane f in the cylinder x² + y² = 1. Find a formula for the highest point on the trace of a general plane f in the cylinder x² + y² = 1. [Hint: At least try it for one other particular plane, say f(x,y) = 2x + y, then see if you can figure out how to generalize in this.]