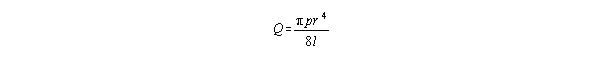Calculus IV Problem Set 1 Spring 1999 Due 1/29/99

 
 
1. [Attachment] Read Spanier's article "Solving Equations Is Not Solving Problems" (Readings for Calculus, A. W. Roberts, 1993). Respond (in less than one page) to either question 2 or question 3. You will be graded on your written presentation (reasoning, structure, support for your position), not on your position (i.e., you can assert things you think Jon will disagree with or take offense at and not worry that you will be marked down or subsequently mistreated).
 
 
 
2. [Stewart 12.3 #92, p. 786] In a study of frost penetration it was found that the temperature T at time t (measured in days) at a depth x (measured in feet) can be modeled by the function

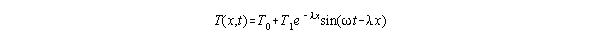
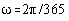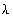where  and  is a positive constant.

(a) Find 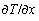. What is its physical significance?
(b) Find . What is its physical significance?
(c) Show that T satisfies the heat equation Tt = kTxx for a certain constant k.
(d) If 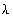 = 0.2, T0 = 0, and T1 = 10, use a computer to graph T(x, t).
(e) What is the physical significance of the term -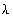x in the expression ?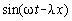
 
 
 
3. [Stewart 12.3 #96, p. 786] If 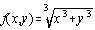, find fx(0,0). [Hint: It isn't actually undefined!]
 
 
 
4. [Based partly on Ellis & Gulick 2nd, #42 p. 757] The time rate Q of flow of fluid through a cylindrical tube (such as a windpipe) with radius r and height l is given by

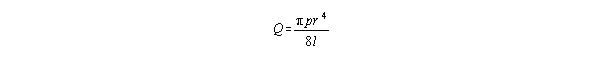
where p is the difference in pressure at the two ends of the tube.

Suppose a field vole's spatial intuition suddenly fails him or her, and he or she falls off a cliff into a large lake. The brave vole struggles to the surface and gulps for air. At the moment when the vole begins to gasp, the vole's windpipe radius increases at the rate of .04 cm/second and the pressure difference increases by .09 atmospheres/second. You can use the typical values of 0.3 cm for the vole's windpipe length and 0.11 cm for the vole's windpipe radius. What is the rate of change of Q with respect to time at this moment?
 
 
 
5. [Stewart Problems Plus #4, p. 830] Let B be a solid box with length L, width W, and height H. Let S be the set of all points that are a distance of at most 1 from some point of B. Express the volume of S in terms of L, W, and H.