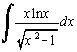Calc IV Lab 1 Key

Calculus IV Lab Assignment 1 Spring 1999 Due 1/17/99

These solutions were taken directly from students' Mathematica notebook submissions.

1. Some Calc I problems are ugly enough that even though you know perfectly well how to do them, it's much more reasonable to let Mathematica do the messy part. Use Mathematica to find the derivative of f(x) =

[Stewart, Problems Plus p. 180 #13b].

Problem 1 Solution

2. You probably don't need to be told that the same goes for some Calc II problems. Use Mathematica to find

[Stewart, Section 7.6 p.472 #66]. The most natural way to do this one by hand involves using a substitution, a property of logs, integration by parts, long division, and finally a trig substitution.

Problem 2 Solution

Integrate[x*Log[x]/Sqrt[x^2-1],x]

3. Consider the function f(x,y) = 10x²y - 5x² - 4y² -x⁴ -2y⁴. This function has three local maxima (sort of hilltop-looking things). Produce a graph that clearly shows all three of these maxima.

Problem 3 Solution 1

Plot3D[10x^2 y - 5x^2 - 4y^2 - x^4 - 2y^4, {x, -4,

 {y, -1, 3}, PlotRange-> {-5,10},PlotPoints -> 50]

-SurfaceGraphics-

Problem 3 Solution 2

ContourPlot[10x^2 y - 5x^2 - 4y^2 - x^4 - 2y^4,

 {x, -5, 5}, {y, -3, 4}, PlotPoints -> 50]

-SurfaceGraphics-

4. See what output Mathematica gives to the command Plot3D[(x^2+y^2)E^(-x^2-y^2), {x,-10,10}, {y,-10,10}]. Although this graph gives a pretty good idea of the overall behavior of this surface -- a flat plain with a big "bump" in the middle -- it's deceptive about the details of this "bump". Experiment with different commands to get a better idea of what's really going on near the origin, and briefly explain why the first graph looked the way it did and how your improvement fixed it.

Problem 4 Solution 1

Plot3D[(x^2+y^2)E^(-x^2-y^2), {x, -5, 5},

 {y, -5, 5}, PlotRange -> {-.5,.5}, PlotPoints -> 50]

-SurfaceGraphics-

-SurfaceGraphics-

In this graph I used "PlotRange" to specify the vertical action of the function. Using "PlotPoints" let me produce a much smoother graph that makes much more sense to look at. This graph finally comes out looking like an ant-hill,(a mound with a dip in the middle). The graph above, #3, was made using the same procedures.

Problem 4 Solution 2

-SurfaceGraphics-

The resolution is not nearly fine enough. We can't see any details. It also seems to be chopping off the top of the graph. Let's zoom in to get a better picture.

-SurfaceGraphics-

Better, but we can't see what's in the hole. Let's cut it in half and see the cross section.

-SurfaceGraphics-

That's better. Now we know it dips down to zero at the origin.

Problem 4 Solution 3

Plot3D[(x^2+y^2)E^(-x^2-y^2),{x,-3,3},{y,-3,3} ,PlotPoints->100, Mesh->False]

-SurfaceGraphics-

4. The first graph did not portray an accurate representation of the
graph because it gave a view point that was too far away and it didn't
have enough detail. I fixed this by increasing the number of plotted
points to 100 and making my viewing window smaller.

5. See what output Mathematica gives to the command Plot3D[Sin[x]Sin[y], {x,-7Pi,7Pi}, {y,-7Pi,7Pi}]. Is this actually a good depiction of the function? Explain what's going on, and find a command that produces a better graph.

Problem 5 Solution 1

Plot3D[Sin[x]Sin[y], {x, -7Pi, 7Pi}, {y, -7Pi, 7Pi}]

-SurfaceGraphics-

Plot3D[Sin[x]Sin[y], {x, -2Pi, 2Pi}, {y, -2Pi, 2Pi}

 PlotRange -> {-1,1}, PlotPoints -> 30]

-SurfaceGraphics-

The first graph is not an accurate depiction of the function because it shows valleys along the x and y axes. The z value at every point along these axes is 0 and since it is not plotting very many points (due to the large scale) it seems to average out the values and show these valleys that don't belong on the graph. The first graph also displays the peaks as jagged and abrupt, which is not the case. Therefore, by zooming in a little on the x and y axes, zooming out on the z axis, and adding to the number of plotted points, we get a more accurate depiction of the function. We see that the lines along the x and y axes don't cause the valley effect that is depicted on the first graph. These operations also serve to smooth out the graph to show that the peaks are smooth and gradual.

Problem 5 Solution 2

Plot3D[Sin[x]Sin[y], {x,-7Pi, 7Pi}, {y, -7Pi, 7Pi}]

-SurfaceGraphics-

This command produces an inaccurate graph whose height appears as a tiny fraction of the function's actual height (one). It is apparently a problem of resolution, since the graph changes dramatically with the number of plot points. The given command uses fifteen plot points; the distribution of these points across the given ranges of x and y must fall in odd places (nearly at zero) that, when simply connected to each other, do not represent the true nature of the function. By increasing the number of plot points and narrowing the ranges of x and y, the following command produces a better graph:

Plot3D[Sin[x]Sin[y],

 {x, -2Pi, 2Pi}, {y, -2Pi, 2Pi}, PlotPoints -> 50]

-SurfaceGraphics-