Each problem is worth 2 points.

For problems 1-6:

• Let C₁ be the line segment from (2,0) to the origin.
• Let C₂ be the path made up of a counterclockwise arc of a circle (centered at the origin) of radius 2 beginning at (2,0) and ending at (0,2), followed by the line segment from (0,2) to the origin.
• Let C₃ be the path made up of a clockwise arc of a circle (centered at the origin) of radius 2 beginning at (2,0) and ending at (0,-2), followed by the line segment from (0,-2) to the origin.

• Let F(x,y) = xi + yj.
• Let G(x,y) = <-y,x>.

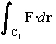2. Use the formula from section 14.2 to compute .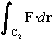
 

3. Use the formula from section 14.2 to compute .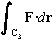
 

4. Use the formula from section 14.2 to compute .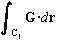
 

5. Use the formula from section 14.2 to compute .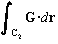
 

6. Use the formula from section 14.2 to compute .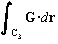
 

7. Do Stewart 14.3 #10.
 

8. Do Stewart 14.3 #12.
 

9. Do Stewart 14.3 #20.
 

10. Which of problems 1-6 could have been done by the Fun. Theorem for Line Integrals? Compute the(ir) values by the Fun. Theorem.