1. Compute![]() for a path beginning at (3,0) and ending at (0,-3).
for a path beginning at (3,0) and ending at (0,-3).
Notice that we're not given any specifics about what sort of path -- a big clue that path doesn't matter, because the Fundamental Theorem for Line Integrals applies.
We try to find a potential function. Taking the antiderivative with respect to x of the coefficient of i gives 3x2y. This also has, as its partial derivative with respect to y, the coefficient of j, so we conclude that f(x,y) = 3x2y is a potential function for this vector field.
Then by the Fun. Thrm. for Line Integrals we just
compute f(0,-3) - f(3,0) = 0 - 0 = 0, so this is the value of the line
integral we started with.
2. Compute![]() for a path C given by r = <2+3t, 1-5t> for t between
0 and 1.
for a path C given by r = <2+3t, 1-5t> for t between
0 and 1.
We can try using the Fun. Thrm. for Line Integrals, hoping for that easy way, but it doesn't apply here because there's no potential function (we can confirm this by noting that the partial of the coefficient of i with respect to y is 2y, which is different from the y we get as the partial with respect to x of the coefficient of j).
So we go through the usual steps for computing
a line integral. The path is already parametrized for us. F(r(t))
= <(1-5t)2, (2+3t)(1-5t)>, and r'(t) = <3, -5>.
Then the integral we're asked about is equivalent to 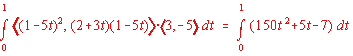 = 45.5.
= 45.5.
Boy, that path sure looks hard to parametrize. Lucky for us we don't have to, since the Fun. Thrm. for Line Integrals applies.
A tip: since the coefficient of j is messier (in the sense of having more terms), start with it when we go to look for a potential function. Antidifferentiate with respect to y to obtain f(x,y) = x2y - 3y2. Check to see that the partial of this is the coefficient of i, and since it is we've found the potential function.
Now evaluate our potential function at the endpoints
of our curve to find f(0,-3) - f(3,0) = -27 - 0 = -27.
2. Compute![]() for a path C which is an arc of a circle (centered at the origin) of radius
3 passing counterclockwise through the first and second quadrants.
for a path C which is an arc of a circle (centered at the origin) of radius
3 passing counterclockwise through the first and second quadrants.
The mixed partials show that no potential function exists, so we have to do it the hard way.
Our path parametrizes as x(t) = 3cos t, y(t) =
3sin t, for values of t between 0 and ![]() .
.
We work out F(r(t)) = <(3cos t)2(3sin t), (3sin t)3>, and r'(t) = <-3sin t, 3cos t>.
Our integral becomes 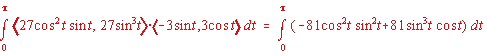 .
This should work out, by way of a simple u = sin t substitution on the
second part and some harder double and half angle identities applied to
the first part, to -81
.
This should work out, by way of a simple u = sin t substitution on the
second part and some harder double and half angle identities applied to
the first part, to -81![]() /8.
/8.