1. Use Green's Theorem to compute
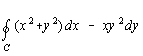 where C is the positively oriented rectangle having vertices (0,0), (1,0),
(1,5), and (0,5).
where C is the positively oriented rectangle having vertices (0,0), (1,0),
(1,5), and (0,5).
1. Use Green's Theorem to compute 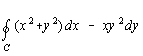 where C is the positively oriented rectangle having vertices (0,0), (1,0),
(1,5), and (0,5).
where C is the positively oriented rectangle having vertices (0,0), (1,0),
(1,5), and (0,5).
The proper conditions apply, since the outside of the rectangle is a simple closed curve (we assume it's oriented the right way) and the partials are all fine.
So by Green's (fun.) Theorem the integral is equal
to 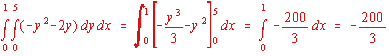 .
.
2. Compute the curl of the vector field F(x,y,z) = x2i - exyzj + cos y k.
We set up the usual determinant 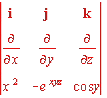 and work it out to get (-sin y + xy exyz)i + (0 - 0)j
+ (-yz exyz - 0)k. If you want to simplify this to (-sin
y + xy exyz)i - yz exyz k you can,
but obviously it's not much of an improvement.
and work it out to get (-sin y + xy exyz)i + (0 - 0)j
+ (-yz exyz - 0)k. If you want to simplify this to (-sin
y + xy exyz)i - yz exyz k you can,
but obviously it's not much of an improvement.
3. Compute the divergence of the vector field F(x,y,z) = x2i - exyzj + cos y k.
We do the respective partials and add them up
to get 2x - xz exyz + 0.
1. Compute 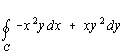 where C is the boundary of the region in the first quadrant between a circle
of radius 1 and a circle of radius 2.
where C is the boundary of the region in the first quadrant between a circle
of radius 1 and a circle of radius 2.
Even though the problem doesn't require it, it's
much
easier to compute this by Green's. It's also much easier to compute the
integral that results if you switch it to polar. It all looks something
like 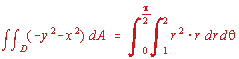 .
This integral is strightforward and comes out to 15
.
This integral is strightforward and comes out to 15 ![]() / 8.
/ 8.
2. Compute the curl of the vector field F(x,y,z) = ![]() .
.
It comes out to 0 (the vector 0, not the number 0). All the coefficients derivatives involved are 0, because the partial derivatives involved cancel each other. For instance, the coefficient of i includes -3xy/(x2+y2+z2)(5/2) minus itself, producing 0. The j and k coefficients work out similarly.
This is actually a good thing -- if this sort
of function is supposed to correspond to stuff coming out of the sun, we'd
rather it come in straight lines without any "swirliness".
3. Compute the divergence of the vector field F(x,y,z) = ![]() .
.
[Note: Vector fields of this sort may be used to model photon flow from a star or neutrino flow from a black hole. Wow.]
Remember the quotient rule? Probably the least
error-prone way to work this is by thinking of the coefficients as (for
instance in the case of i): ![]() .
Then the derivative is
.
Then the derivative is 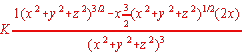 .
This simplifies a lot -- first divide top and bottom by (x2
+ y2 + z2 )1/2 and then collect like terms
to get
.
This simplifies a lot -- first divide top and bottom by (x2
+ y2 + z2 )1/2 and then collect like terms
to get ![]() .
Then it gets cool. That was just the x term. When we add on the partials
of the y and z terms (they look a lot like the x term, just with -2y2
and -2z2 respectively), everything cancels... at least
as long as x, y, and z aren't all zero. So the divergence is 0 everywhere
except at the origin, where its value is a function of K. As with #2, pretty
reasonable considering the context.
.
Then it gets cool. That was just the x term. When we add on the partials
of the y and z terms (they look a lot like the x term, just with -2y2
and -2z2 respectively), everything cancels... at least
as long as x, y, and z aren't all zero. So the divergence is 0 everywhere
except at the origin, where its value is a function of K. As with #2, pretty
reasonable considering the context.